Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Table of Contents
- Ratios
- Simplifying Ratios
- Proportions
- The Rule of Proportions
- Cross Multiplication
- Percents
- Word Problems
Ratios
A ratio is a way to show the relationships between two things. For example, let’s say you have a basket of fruit. There are 7 apples and 12 oranges in the basket. The ratio of apples to oranges is 7 to 12. Ratios can be written in a few different ways.
A ratio can be written:
1) Using the word “to”, for example, 7 to 12
2) With a colon, such as 7:12
3) As a fraction, like this: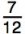 
Using the example above, we can create a ratio of apples to the total amount of fruit, as well as a ratio of oranges to the total amount of fruit.
The ratio of apples to the total amount of fruit can be expressed in the following three ways:
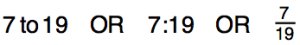
1. What is the ratio of oranges to the total amount of fruit as a fraction?
2. What is the ratio of oranges to the total amount of fruit.
3. What is the ratio of oranges to the total amount of fruit.
All three method of writing a ratio are correct.
Let’s practice ratios.
The local softball team has played 22 games this season. The team has 17 wins and 5 losses.
4. What is the ratio of wins to losses?
5. What is the ratio of losses to total games?
Simplifying Ratios
Some ratios share a Greatest Common Factor (GCF). This means that both numbers in the ratio can be divided evenly by some other number. When you divide each number by this GCF, the ratio can be simplified or written in its simplest form.
For example, let’s say a classroom has 9 boys out of 21 students in the class. The ratio of boys to total students can be written as 9:21.
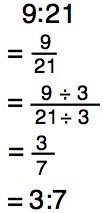
This ratio can be simplified. Both 9 and 21 can be divided by 3.
Using 3 as our GCF, we divide each number by 3 and get a ratio of 3:7 in simplest form.
Let’s practice.
6. What is the ratio of 4:12 in simplest terms?
7. What is the ratio of 24:6 in simplest terms?
8. What is the ratio of 12:30 in simplest terms?
Proportions
Earlier we learned that the ratio 9:21 could also be represented in simplest terms as 3:7. What we are saying is that 9:21 = 3:7. This can also be written in fraction form like this:
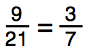
You would read this as 9 over 21 equals 3 over 7. You can also say 9 is to 21 as 3 is to 7.
This concept, that two ratios are equal even though they have different values, is called proportion. A proportion is any statement that follows this form:
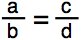
The Rule of Proportions
In any proportion where 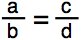is true,
then (a)(d) = (b)(c).
This rule can be used to check whether a proportion is true or not.
Let’s take a look at some examples.
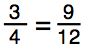
In this example, if we apply our rule, we would say 3 • 12 = 4 • 9. In doing the math, it turns out that 3 • 12 = 36, and 4 • 9 = 36.
So, 36 = 36, and this statement is a true proportion.
Here’s another example.
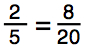
In this example, the rule says that if this is true, then 2 • 20 = 5 • 8. In checking, 2 • 20 = 40, and 5 • 8 = 40.
So, 40 = 40, and this statement is a true proportion.
Let’s look at one last example.
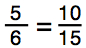
In this example, the rule says that if this is a true proportion, then 5 • 15 = 6 • 10. In checking, 5 • 15 = 75, and 6 •10 = 60.
75 = 60 is not true. Therefore, this statement is not a true proportion.
Let’s practice.
9. This is a true proportion?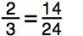 
10. This is a true proportion?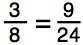 
11. This is a true proportion?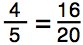 
12. This is a true proportion?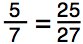 
Cross Multiplication
The process we used to multiply to see if a proportion is true is called cross multiplication. The numbers from the ratio or fraction we multiply are called cross products.
In the problem 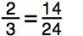the cross products are (2)(24) and (3)(14).
You can use cross multiplication to help you find a missing number. Let’s see this in more detail.
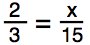
In this statement, we are missing a number, currently replaced by x. We will use cross multiplication to help us solve for x.
If we set up our cross products we get this:
2 • 15 = 3 • x
Multiplying this out we get:
30 = 3x
Now, to get x by itself, we need to divide both sides by 3:
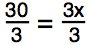
30 divided by 3 = 10, and 3x divided by 3 leaves us with x. Therefore,
10 = x
Now let’s check our work by substituting 10 back into our original statement to see if we are correct.
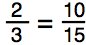
If we use our rule of proportions that we learned earlier, 2 • 15 = 3 • 10, we can check our answer.
2 • 15 = 30
3 • 10 = 30
Therefore, 30 = 30, and our answer is correct.
Now solve for x in these practice problems.
13. 
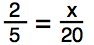
14. 
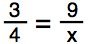
15. 
16. 
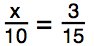
Percents
Percents are actually ratios. The word “percent” means “per hundred.” For example, if we say 25%, we are saying 25 out of 100. As you have learned, ratios can be written as a fraction. So, 25% as a fraction looks like this:
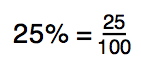
Let’s work through a problem to determine what percentage of squares in a grid are colored yellow.
Take a look at the grid below, which is made up of 100 squares. What percent of the grid is colored yellow?
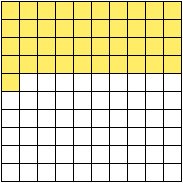
Counting up the yellow squares, we see that we have 4 rows of 10, plus one additional square.
4 • 10 = 40; 40 + 1 = 41
That gives us 41 squares that are colored yellow out of 100. Putting this into a fraction, we get:
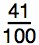
How do we represent this as a percent? 41 out of 100 is 41%.
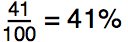
17. What percent of this grid is colored green? 
18. What percent of this grid is colored blue? 
Word Problems
There are many kinds of word problems that use ratios, proportions, and percents.
Any problem that gives you information and then asks you to solve for something that is proportional can be done with ratios and cross multiplication.
For example, let’s look at this problem.
If 40 pounds of apples cost $24, how much do 100 pounds of apples cost?
This can be solved as a proportion:
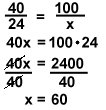
The cost of 100 pounds of apples is $60.
In a problem like this, the ratios in the proportion must be set up identically. If apples are on top in one ratio then apples must be on top in the other ratio.
Let’s do another one. If it takes 10 pounds of flour to make 20 cakes, how much flour would it take to make 5 cakes?
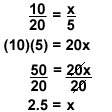
Now, you do a few.
19. If it takes 1 gallon of paint to paint 100 square yards, how much paint would you need to cover 1,200 square yards?
20. If washing one load of laundry takes 30 gallons of water, how much water does 6 loads of water take?
Another kind of problem that uses percents and proportions are ones that involve sales and discounts. Here is a proportion you can use for this:
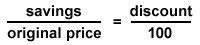
And we know that:
Let’s use this to solve some problems.
David wants to buy a new pair of shoes. The price is $75 but they are 25% off. How much will he pay after the discount?
$56.25 is how much he will pay after the discount.
There is a book that is marked as being priced $20 off. The original price was $80. How much of a discount is that?
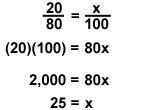
The discount is 25%.
Now, you practice some of these.
21. Mrs. Juarez is buying a new couch. The original price was $800, but it is on sale with a 30% discount. How much will she pay?
22. The original price for a car was $5,000, but now it’s on sale for $4,400. What percentage of discount is this?