Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Monroe 2-Orleans BOCES.
Table of Contents
Integers
An integer is a whole number. It can be positive or negative. Positive numbers are bigger than zero. Negative numbers are smaller than zero. We use negative numbers to talk about things that are less than zero. For example, if the temperature is below zero, it is negative. -30 degrees is very cold! If a football player loses yardage on a run, he runs for negative yardage. A spot on the earth that is below sea level has a negative elevation.
Here is a number line with positive and negative numbers.
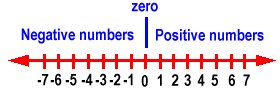
Positive numbers are to the right of zero. Negative numbers are to the left of zero. Negative numbers always have a negative sign (-) in front of them. For example, -2 means negative 2.
Opposite numbers are the positive and negative of the same number. For example, 3 and -3 are opposite numbers.
The absolute value of a number is the distance it is from zero. We can find the absolute value by taking off the negative sign if there is one. The absolute value of –3 is 3. The absolute value of 7 is 7.
We write the absolute value using bars. For example, |-8| means the absolute value of -8.
Now let’s practice.
1. Is 560 an integer?
2. Is ½ an integer?
3. Numbers to the right of zero on the number line are:
4. Numbers to the left of zero on the number line are:
5. What is the opposite number of 2?
6. What is the opposite number of -5?
7. What is the absolute value of 6?
8. What is |-10|?
Comparing Integers
We can compare the size of different integers. For positive numbers, larger numbers are bigger than small numbers. For example, 10 is larger than 5. 10 is farther to the right of zero on the number line, which means it is larger.
For negative numbers, though, the opposite is true. The higher the negative number, the farther to the left it is from zero. That means that it is smaller. -10 is smaller than -5.
All negative numbers are smaller than positive numbers.
We use the symbols >, <, and = to compare the sizes of integers.
> means greater than.
< means less than.
= means equal.
You can remember the > and < signs by remembering that the open end of the sign always points toward the bigger number. For example:
5 > 3
This tells us that 5 is greater than 3. (Note that the bigger end of the sign opens toward the bigger number.)
-6 < -3
-6 is less than -3. (Because these two numbers are negative, the higher one or the one farther to the left on the number line is larger.)
|-7| = 7
The absolute value of -7 is 7. This is equal to the 7 on the other side.
6 > |-5|
6 is greater than 5. (5 is the absolute value of –5.)
Now, you can practice some.
9. Choose the correct statement.
10. Choose the correct statement.
11. Choose the correct statement.
12. Choose the correct statement.
A) -9 < -5
B) -9 > -5
C) -9 = -5
13. Choose the correct statement.
A) |-8| < 8
B) |-8| > 8
C) |-8| = 8
Adding and Subtracting Integers
To add positive integers, we move to the right on a number line. For example,
2 + 3 = 5
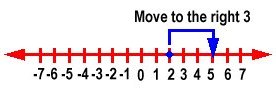
For, -4 + 6 = 2
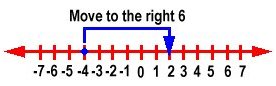
To add negative numbers, we move to the left on a number line. For example, -3 + -4 = -7
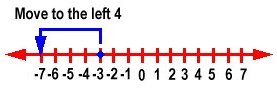
You can see from the above that when we add two positive numbers, we add the numbers and the answer is positive.
When we add a positive and a negative number, we subtract and the answer takes the sign of the number with the largest absolute value.
When we add two negative numbers, we add the numbers and the answer is negative.
Rules for adding integers:
Adding numbers with the same sign
Add the absolute values and keep the sign the same as the numbers
Adding numbers with different signs
Subtract the absolute values and take the sign of the number with the largest absolute value
Here are some more examples:
3 + 3 = 6
(Both numbers have the same sign, so we add and keep the sign the same.)
-4 + -7 = -11
(Both numbers have the same sign, so we add and keep the sign the same.)
-8 + 3 = -5
(Numbers have different signs, so we subtract and take the sign of the largest absolute value.)
12 + -4 = 8
(Numbers have different signs, so we subtract and take the sign of the largest absolute value.)
Practice these on your own.
14. -8 + -2 =
15. -5 + -2 =
16. -6 + 2 =
17. 10 + -3 =
18. -12 + -1 =
19. -4 + 2 =
Now, let’s look at subtracting integers. Subtracting an integer is the same as adding its opposite.
For example:
5 – 2 =
is the same as
5 + -2 = 3
4 – -3 =
is the same as
4 + 3 = 7
-8 – 5 =
is the same as
-8 + -5 = -13
Another short cut that will help you with subtraction is that if you subtract a negative, you can cancel both negative signs like this:
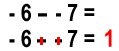
Practice these problems on your own. Begin by rewriting the problem as an addition problem. Then find the answer using the rules you learned for addition.
20. 2 – 4 =
21. -5 – 7 =
22. 9 – -8 =
23. 8 – 10 =
Multiplying and Dividing Integers
When we are multiplying integers, we multiply the absolute values and then give the answer a sign according to these rules:
Multiplying two positive numbers
Multiply and the answer is positive
Multiplying one positive and one negative number
Multiply and the answer is negative
Multiplying two negative numbers
Multiply and the answer is positive
We can write multiplication with parentheses, for example:
(3)(4) = 12
or we can use a dot, for example:
3 • 4 = 12
Here are some examples of multiplying integers:
8 • 7 = 56
(A positive times a positive equals a positive.)
(8)(-4) = -32
(A positive times a negative equals a negative.)
-9 • -9 = 81
(A negative times a negative equals a positive.)
Now, you try some:
24. (-3)(10) =
25. 8 • -4 =
26. -5 • -6 =
27. (-12)(2) =
28. (-7)(-6) =
The rules for dividing integers are similar to multiplying.
Dividing two positive numbers
Divide and the answer is positive
Dividing one positive and one negative number
Divide and the answer is negative
Dividing two negative numbers
Divide and the answer is positive
Practice some of these:
29. 50 ÷ -5 =
30. -40 ÷ -8 =
31. 64 ÷ 8 =
32. -72 ÷ -9 =
33. 80 ÷ -8 =