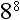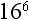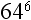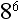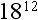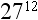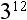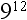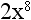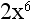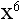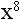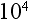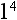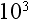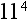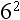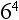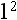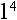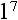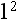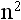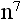Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Table of Contents
Exponents
An exponent is a short way to write how many times a number is multiplied by itself. For example, look at the following number:
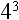
This means that 4 is multiplied by itself three times. Without using exponents, this same number looks like this:
4 • 4 • 4
Four times 4 is 16. Sixteen times 4 is 64.
So, 4 • 4 • 4 = 64.
Therefore, 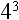= 64
A number that has an exponent is said to be “raised to the power” of that exponent. So, in our example, we say it is “four raised to the third power.”
In our example, the 4 is called the base, and the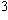 
is called the exponent.
Let’s practice this.
1. How would 3 • 3 • 3 • 3 • 3 be represented in exponent form?
2. How would 2 • 2 • 2 • 2 be represented in exponent form?
3. How much is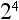 
?
4. What is the exponent in the number 
?
5. What is the base in the number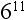 
?
Rules of Exponents
Rule 1: Any number raised to the power of 1 is equal to that number.
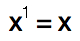
Therefore,
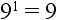
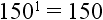
Rule 2: Any number raised to the power of zero (except zero itself) equals 1.
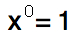
Therefore,
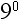
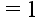
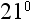
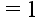
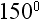
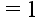
Let’s practice. Select the answer to each problem below.
6. What is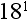 
?
7. What is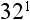 
?
8. What is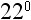 
?
9. What is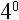 
?
Rule 3: When multiplying numbers with the same base, the exponents are added.
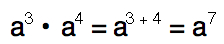
Let’s look at this in more detail. Say we have the following numbers being multiplied together:
According to our rule, we can do this:
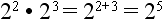
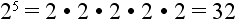
In looking at our original problem
we can work it out this way:
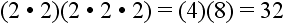
This shows us that our rule works. We get 32 by applying the rule and also by working out the multiplication.
Rule 4: When dividing numbers with the same base, the exponents are subtracted.
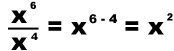
Let’s look at another example for this: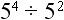 
According to the rule:
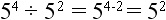
Let’s work out the problem:
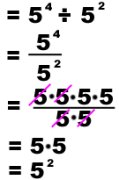
This gives us the same answer, so we have proved that the rule works.
Let’s try some of these:
10. 
A) 
B) 
C) 
D) 
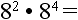
11. 
A) 
B) 
C) 
D) 
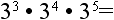
12. 
A) 
B) 
C) 
D) 
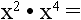
13. 
A) 
B) 
C) 
D) 
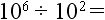
14. 
A) 
B) 
C) 
D) 
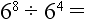
15. 
A) 
B) 
C) 
D) 
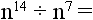
Scientific Notation
Do you know how far away the earth is from the sun? 93,000,000 miles!
Do you know the mass of the earth in kilograms?
It’s 6,000,000,000,000,000,000,000,000 kilograms!
To work with such large numbers without writing all these zeroes, scientists came up with a shorter method. This method is called scientific notation.
Scientific notation looks like this. The number 234,000,000,000 is written as:
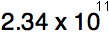
To make the scientific notation of a number, you put a decimal point after the first digit and remove all the zeros.
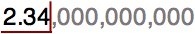
This first part of the number is called the coefficient. This number must always be greater than 1, and less than 10.
The second part of the number is known as the base. The base is always 10 for scientific notation with an exponent. The exponent is determined by counting all the digits to the right of the decimal.
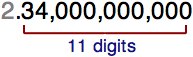
To change a number from scientific notation back to standard form, just move the decimal to the right the number of places of the exponent.
Let’s practice.
16. In scientific notation, what is the coefficient for the number 831,000,000?
17. What is the exponent for the number 831,000,000?
18. In scientific notation, what is the coefficient for the number 214,000,000,000?
19. What is the exponent for the number 214,000,000,000?
20. How is this number written without scientific notation (in standard form):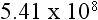 
?
21. What is the base in any number with scientific notation?