
Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Monroe 2-Orleans BOCES.
Table of Contents
Factoring – Using the Distributive Property
A factor is a number that can be divided into another number evenly. For example, the factors of 6 are 1, 2, 3, and 6. All of these numbers can be divided evenly into 6.
We can look for common factors within a math statement. We use factoring to find these common factors. Take, for example, the statement:
3x + 3y
In the above statement, the number 3 is a common factor between the two terms in the statement, 3x and 3y. We can divide 3 into both numbers evenly. This is also called “factoring out” 3.
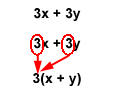
Finding the common factor allows us to apply the Distributive Property to the statement. The Distributive Property applies multiplication to an existing addition statement. It means that a number outside the parentheses of an addition problem can be multiplied by each number inside the parentheses. Or in the opposite case, a common factor can be factored out and written outside the parentheses.
So, with 3 as our common factor, the statement 3x + 3y becomes 3(x + y), or 3 multiplied by “x + y.”
You can always check your work by multiplying the numbers in your answer. For 3(x + y), you can check your work as follows:
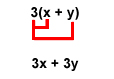
Here is another example:
2a + 6b
In the above statement, the common factor can be found by breaking down the numbers.
In the first term, 2a, the 2 can be factored down to 2 •1.
In the second term, 6b, the 6 can be factored down to 2 • 3.
You can now see that 2 is the common factor, and we can now apply the Distributive Property.
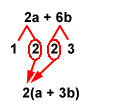
So, the statement 2a + 6b can be written as 2(a + 3b), or 2 multiplied by “a + 3b.”
Here is one more example:
5xy + 15xz
In the above statement, the common factor includes the variable, x, because it is common between the two terms in the statement. Any letter variable that appears in both terms can be factored out.
Now, let’s factor out the numbers:
5 = 5 • 1
15 = 5 • 3
We find that 5 is part of the common factor. The other part, x, makes the common factor 5x.
So, 5xy + 15xz can be written as 5x(y + 3z).
To check the work:
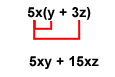
This is our original statement, 5xy + 15xz, so our work is correct.
Greatest Common Factor (GCF)
There will be times when you see a statement where there is more than one common factor. For example, in the statement 4x + 12y, you can break down the numbers as follows:
4 = 2 • 2
12 = 2 • 6
So, at first glance, it may appear that 2 is the common factor. Actually, there is a larger number that can serve as the common factor.
4 = 2 • 2
12 = 2 • 2 • 3
As seen here, the number 12 actually breaks down to 2 • 2 • 3. Given this, the common factor between these terms is actually 2 • 2, or 4.
So, the breakdown looks more like this:
4 = 4 • 1
12 = 4 • 3
In this example, the number 4 is the Greatest Common Factor, or GCF. So, the statement 4x + 12y can be written as 4(x + 3y).
Now let’s practice.
1. Find the common factor in 7a + 7b.
2. Find the common factor in 5x + 5y.
3. Find the common factor in 3x + 12y.
4. Find the common factor in 2a + 14b.
5. Find the common factor in 3ab + 4ac + 5ad.
6. Find the common factor in 5ab + 10ac + 20az.
7. Find the greatest common factor in 4x + 16y.
8. Find the greatest common factor in 8x + 20y + 16z.
9. Find the greatest common factor in 12bc + 6bd + 36be.
Now, let’s factor the following statements using the Distributive Property:
10. 2x + 2y
11. 5a + 5b
12. 3x + 6y
13. 7m + 21n
14. 9x + 36y
15. 4a + 6b + 8c
16. 4g + 16h + 8i
17. 5ab + 15ac + 25az
18. 6abc + 18abd + 36abe