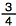Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Monroe 2-Orleans BOCES.
Table of Contents
- Understanding Factors and Products
- Multiplying Decimals
- Using Estimation
- Problem Solving
- Dividing Decimals
- Decimals and Percents
- Decimals and Fractions
Understanding Factors and Products
Before we start, let’s review some math terms. When we multiply two numbers to come up with an answer, the numbers that are used for the multiplication are called factors. The answer is called the product.
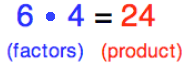
In this example, the numbers 6 and 4 are factors, the number 24 is the product.
Let’s practice identifying factors and products.
1. In the statement (8)(4) = 32, what is the product?
2. In the statement 7 • 5 = 35, what is the product?
3. In the statement 10 • 8 = 80, what are the factors?
4. In the statement (9)(11) = 99, what are the factors?
5. In the statement 5 • 6 = 30, which of these is NOT a factor?
Multiplying Decimals
Multiplying decimals is just like multiplying whole numbers. The only difference is that the decimal places must be carried from the factors to the product. Let’s look at an example.
If we multiply 15 by 11, it looks like this:
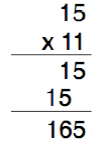
Now, if we multiply numbers that have decimals, such as 1.5 • 1.1, it looks like this:
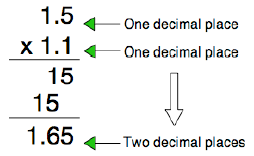
The multiplication process for the two examples above is the same; the only difference in the second example is what we do with the decimals.
When multiplying decimals, we look at the decimal in each factor and count how many decimal places each is from the right.
In this case, there is a total of two decimal places (one from 1.5 and the other from 1.1). So, in our product, we put the decimal two places from the right, arriving at 1.65.
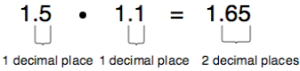
Let’s look at another example:
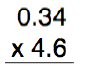
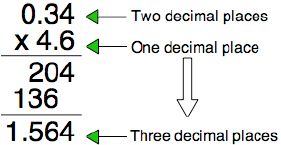
In this case, the first factor, 0.34, has the decimal two places from the right. The second factor, 4.6, has the decimal just one place from the right. This gives us a total of three decimal places.
We multiply as usual, ignoring the decimals, and then move the decimal over three places in the answer.
Our answer looks like this:
Let’s practice, use a paper and pencil to solve the problems. Check below:
6. (4.8)(7.7) =
7. (6.2)(9.1) =
8. 1.06 • 8.4 =
9. 2.26 • 3.7 =
10. 5.34 • 0.38 =
Using Estimation
In working with decimals, it is often helpful to use estimation to see if your answer is reasonable. Let’s use this example
7.41 • 2.7
To estimate, we can round off the numbers to the closest whole number. In this case:
7 • 3
If you multiple 7 times 3, you get 21. So, 21 is an estimate for the correct answer. When we multiply, our answer should be near 21.
In working out 7.41 • 2.7, we get the answer 20.007 (which would round off to 20, the closest whole number). This answer is reasonable because it is very close to the estimate of 21.
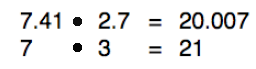
If you put the decimal in the wrong place and came out with 200.07 (rounded off to 200), this would not be a reasonable answer.
You would know that a mistake was made.
In this way, estimation helps us to check our work.
Here are some problems with possible answers provided. Use estimation to determine which answer seems the most reasonable.
11. 3.1 • 7.9 =
A) 24.49
B) 0.2449
C) 2.449
D) 244.9
12. 8.2 • 9.1 =
A) 74.62
B) 746.2
C) 7.462
D) 0.7462
13. 12.3 • 4.9 =
A) 60.27
B) 602.7
C) 6.027
D) 0.6027
14. 1.9 • 6.2 =
A) 0.1178
B) 11.78
C) 117.8
D) 1.178
15. 6.08 • 8.34 =
A) 5070.72
B) 507.072
C) 50707.2
D) 50.7072
16. 5.84 • 3.23 =
A) 18.8632
B) 188.632
C) 1.88632
D) 1886.32
Below are some problems where the answer is already shown, but without any decimal placement. Count the decimal places in the factors to determine where the decimal place should go in the product.
17. Pick the answer with the correct decimal placement: 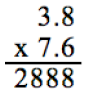
A) 2.888
B) 2888
C) 288.8
D) 28.88
18. Pick the answer with the correct decimal placement: 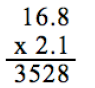
A) 3.528
B) 35.28
C) 352.8
D) .3528
19. Pick the answer with the correct decimal placement: 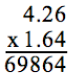
A) 698.64
B) 6986.4
C) 69.864
D) 6.9864
20. Pick the answer with the correct decimal placement: 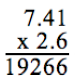
A) 19.266
B) 1.9266
C) 192.66
D) 19266.
Problem Solving
Let’s apply what we have learned about multiplying decimals to word problems.
“Johnny makes $4.75 per hour at his work. If he works 6 hours, how much money will he earn?”
To set this problem up, we need to determine what facts are needed to find the answer.
The first fact is that Johnny gets $4.75 for every hour he works.
The second fact is that Johnny works 6 hours.
So, in order to solve our problem, we need to multiply Johnny’s hourly rate of pay ($4.75) times the number of hours he works (6). The set up of our problem should look like this:
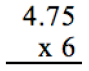
By doing our multiplication, and by making sure we place our decimals correctly, we get the following answer.
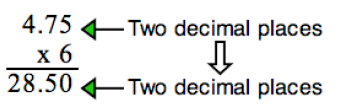
Therefore, Johnny makes $28.50 for six hours of work.
Let’s practice some more word problems. Remember to use your estimation skills to help you check your answers to see if they are reasonable.
21. Tina’s cat weighs 2.6 kilograms. Her dog weighs 4 times as much as her cat. How much does her dog weigh in kilograms?
22. Baby Isabel plays with blocks. Each block is 3.7 inches tall. She has a collection of 41 blocks. If she could stack all of the blocks up one on top of the other, how many inches tall would her tower of blocks be?
23. Carrie likes to buy t-shirts at the local clothing store. They cost $9.95 each. One day, she bought 25 t-shirts. How much money did she spend?
24. Jim rides the bus to and from school each day. A one-way trip is 8.12 kilometers. How many kilometers does he travel in 3 days?
Dividing Decimals
Dividing decimals is just like regular division. The difference is that you have to watch the decimal points. Let’s first look at a division problem with whole numbers.
Here’s a regular division problem with just whole numbers, 138 ÷ 3.
In this problem, 3 is the divisor (the number you are dividing by) and 138 is the dividend (the number being divided).
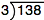
We work the problem out like this:
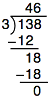
Our answer is 46. In division, the answer is called the quotient.
We can check our work by multiplying the quotient by the divisor, or (46)(3). This gives us 138, the number we started with as our dividend.
Our work has been done correctly.
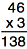
Let’s look at this same problem with 138 changed to 13.8. We are now dividing into a number with a decimal point.
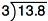
Here, the work to solve the problem is the same as the previous example, we just need to place the decimal point directly above in the quotient.
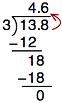
So, 13.8 ÷ 3 equals 4.6, and we can check this by multiplying (4.6)(3). We get 13.8.
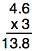
What if the divisor in our problem has a decimal point? Let’s see what this looks like with the following example.
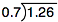
In order for us to work out this problem, we must change our divisor to a whole number. We do this by moving our decimal point to the end of the number. We need to move it to the right as many places as necessary to make a whole number.
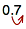
In this case, with the divisor as 0.7, we only need to shift the decimal point one place to the right to make it a whole number.
Now, in order to do this without changing the result of our problem, we must move the decimal point in the dividend the same number of places.
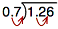
So, after shifting our decimals, our problem looks like this:
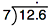
Now, let’s work out the problem. Remember to move the decimal straight up in the answer.
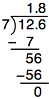
So, 1.26 ÷ 0.7 = 1.8
Once again, we can check our answer. We multiply (1.8)(0.7) (our original divisor), and arrive at 1.26 (our original dividend).
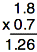
Let’s practice.
25. 22.5 ÷ 3 =
26. 3.65 ÷ 5 =
27. 4.26 ÷ 0.3 =
28. 25.64 ÷ 0.02 =
Decimals and Percents
Percents can be written as decimals using the following rules:
1) To change a percent to a decimal, move the decimal point two places to the left.
2) To change a decimal to a percent, move the decimal point two places to the right.
Let’s look at some examples:
To change 5 percent (also written as 5%) to a decimal, we need to move the decimal point two places to the left. Although we don’t see the decimal point in the number 5, because it is a whole number, the decimal is to the right of 5.
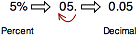
Here’s another example.
In this problem, we will change 28% into a decimal.
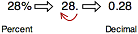
Let’s practice.
Change the following percents to decimals.
29. 54% =
30. 365% =
31. 2% =
32. 21.3% =
We can also change decimals to percents, using the second rule we learned: “To change a decimal to a percent, move the decimal point two places to the right.”
So, if we are given the number 0.37 and are asked to change it to a percentage, it would look like this:
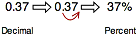
Let’s practice. Change the following decimals to percents.
33. .02 =
34. .89 =
35. 1.35 =
36. .005 =
Decimals and Fractions
Fractions are really division problems. The number on the top of the fraction (the numerator) is divided by the number on the bottom (the denominator).
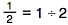
So to change a decimal to a fraction, you just divide the number on top by the number on the bottom. You will need to put the decimal point in as you do this.
To change 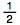 to a decimal, divide 1 by 2:
to a decimal, divide 1 by 2:
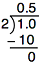
Therefore,
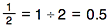
Try changing these fractions into decimals.
37. 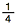
38. 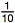
39. 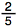
40.