Published by K12 Handhelds, Inc.
Portal, AZ
www.k12handhelds.com
Copyright © 2008 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Wayne Township School System.
Table of Contents
- Overview
- Graphing Inequalities
- 1-Step Addition and Subtraction Inequalities
- 1-Step Multiplication and Division Inequalities
- 2-Step Inequalities
Overview
An inequality is a mathematical statement that tells about two expressions that are not equal. Inequalities may show an expression that is greater than or less than something.
These are the symbols used in inequalities:
 Greater than
Greater than
(You can remember this because the bigger, open end is first.)
 Less than
Less than
(You can remember this because the smaller, closed end is first.)
 Greater than or equal to
Greater than or equal to
(The line under the symbol means equal to.)
 Less than or equal to
Less than or equal to
When we read an inequality, we read it from left to right.
Here are a few examples.
10 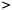 7
7
Ten is greater than 7.
x 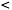 9
9
x is less than 9.
p 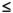 5
5
p is less than or equal to 5.
y 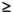 4
4
y is greater than or equal to 4.
Try reading these on your own:
x 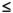 9
9
10 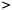 2
2
t 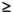 3
3
k 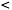 2
2
9 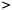 6
6
m 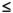 2
2
Often, it is easiest to put the variable, such as x, on the left side of the equation.
An inequality can be rewritten in the other direction; just make sure you flip the inequality sign.
For example,
3 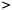 x
x
can be rewritten as
x 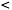 3.
3.
An easy way to remember this is to make sure the small end of the symbol is pointing at the same number. In this case, the small end of the < symbol is pointing at the x in both cases.
To translate words into an inequality, first decide what symbol to use. Are the things being described greater than, less than, greater than or equal to, or less than or equal to something?
Then figure out which expression is larger and put that on the bigger (open) end of the symbol. Put the other expression on the other side. Remember that an unknown can be represented with an x or another letter variable.
For example, let’s write the expression “x is less than three” as an inequality. The words “less than” tell us to use a < sign. x is less than, so that goes on the closed end of the symbol. The inequality is:
x 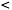 3
3
How about “Buying 10 gallons of gas will cost more than $30” as an inequality?
“More” tells us to use a >. The price per gallon is unknown, so we’ll use x for that. The price of 10 gallons (10x) will be more than $30, so we have:
10x 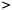 30
30
How would you write “All three cats together weigh less than 10 pounds” as an inequality? Here’s a hint: We don’t know the weight of any of the cats (and they don’t necessarily weigh the same amount.) Here is the inequality:
a + b + c 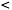 10
10
(You could use any three letters for variables as long as they are different from each other.)
Let’s do one more. Write this as an inequality: “The price of the car is $3,000 or less.”
The answer is:
p 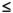 3,000
3,000
We need to use the less than or equal to symbol because the sentence said “$3,000 or less.”
Let’s practice some of these now.
Practice
1. Which symbol means less than?
2. Which symbol means greater than or equal to?
3. Which symbol means less than or equal to?
4. Which symbol means greater than?
5. How would you write “three is greater than zero”?
6. How would you write “x is less than or equal to 9”?
7. How would you write “m plus four is less than 6”?
A) m + 4  6
6
B) m + 4  6
6
C) m + 4  6
6
D) m + 4  6
6
Choose the equivalent inequality.
Graphing Inequalities
Graphing simple inequalities is easy. A simple inequality has the variable (x or some other letter) on the left and a number on the right.
To begin, put a dot on the number line for the number given. If the inequality symbol is 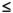 or
or 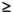 , use a regular solid dot. If the inequality symbol is < or >, use an empty dot.
, use a regular solid dot. If the inequality symbol is < or >, use an empty dot.
For 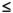 or or 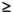 , use , use  . .For < or >, use  . .
|
First, put a dot on the number line at the point of the number on the right of the inequality. Then draw a line with an arrow all the way to the right if the symbol is > or 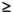 . Draw a line with an arrow all the way to the left if the symbol is < or
. Draw a line with an arrow all the way to the left if the symbol is < or 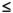 .
.
>  <  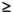  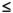 
|
You can remember these by just thinking about what the symbols mean.
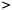 means greater than the number (but not equal to, which is why the dot is empty, because the number itself is not part of the answer).
means greater than the number (but not equal to, which is why the dot is empty, because the number itself is not part of the answer).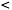 means less than the number (but not equal to, which is why the dot is empty).
means less than the number (but not equal to, which is why the dot is empty).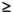 means greater than or equal to the number (which is why the dot is solid).
means greater than or equal to the number (which is why the dot is solid).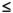 means less than or equal to the number (which is why the dot is solid).
means less than or equal to the number (which is why the dot is solid).
Let’s look a few examples based on these rules.
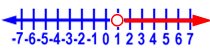
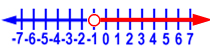
Graph x > 3.
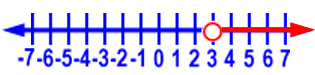
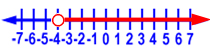
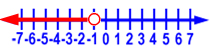
Graph x < -2.
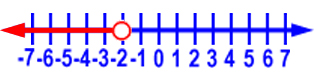
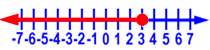
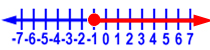
Graph x 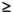 0.
0.
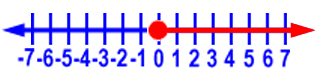
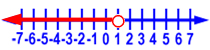
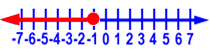
Graph x 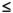 -1.
-1.
Now you try some.
Practice
Choose the correct graph for each inequality.
12. x > -4
13. x  1
1
14. x < 3
15. x > -1
16. x 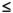 6
6
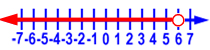
17. What is the correct inequality for this graph?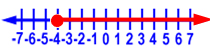
A) x  -4
-4
B) x  -4
-4
C) x  -4
-4
D) x  -4
-4
18. What is the correct inequality for this graph?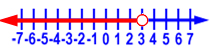
19. What is the correct inequality for this graph?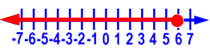
1-Step Addition and Subtraction Inequalities
In an inequality, the variable (x or some other letter) is the unknown. To solve an inequality, we need to find the value of the variable. To do this, we get the variable on one side of the inequality by itself.
We must keep the equation in balance, so whatever we do on one side of the equation, we must do to the other side as well.
To get x by itself, we use inverse operations to get rid of whatever is with x. This means we do the opposite. If something is added to x in the equation, we need to subtract it to get rid of it. If something is subtracted from x, we need to add it to get rid of it. Remember that whatever we do to one side, we do to the other side as well.
Here’s an example. Solve x + 5 > 9.

We can graph this solution this way:

For every inequality you solve, you can check your work by substituting your answer back into the problem to see if it is correct. In this case, we’ll choose a value for x that is > 4. We’ll use 5 and substitute that into the original equation:

We can see that 10 is greater 9, and our check works out.
Let’s do another one. Solve m – 3 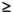 0. Remember that you need to use inverse operations to get the variable by itself.
0. Remember that you need to use inverse operations to get the variable by itself.

The graph of this solution is:

Let’s check our solution by plugging in a number that is greater than or equal to 3. We’ll use 3.
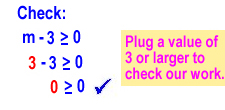
Let’s do one more example. Solve p + 6 < 8.
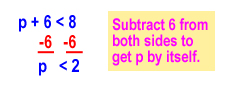
Here is the graph of the solution:
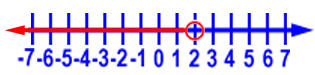
We can check our solution by substituting a value that is less than 2. We’ll use 1.

1-Step Multiplication and Division Inequalities
Let’s take a look at inequalities that involve multiplication and division.
Again, we need to get the variable on one side of the inequality by itself. To keep the equation in balance, whatever we do on one side of the equation, we must do to the other side as well.
To get x by itself, we use inverse operations to get rid of whatever is with x. This means we do the opposite. If something is multiplied by x in the equation, we need to divide by it to get rid of it. If x is divided by something, we need to multiply by it to get rid of it.
The only new step is that if we multiply or divide by a negative number, we need to flip the inequality sign.
Let’s do an example. Solve 6x > 12.

Here is the graph of the solution:
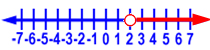
Let’s check our work. We need to substitute in a number for x that is greater than 2. We’ll use 3.

18 is greater than 12, so our check is good.
Since this problem doesn’t involve multiplying or dividing by a negative number, we don’t need to flip the inequality sign.
Let’s do another one. This one has a negative number, so we’ll need to remember to flip the inequality sign. Solve –2t 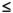 10.
10.

Here is the graph of the solution:
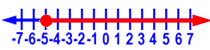
Let’s check our work. We need to substitute in a number for t that is greater than or equal to -5. Let’s use -4.

Let’s do another one that has division in it.
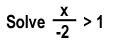
For this problem, we’ll need to multiply by –2 to get x by itself, so we’ll need to reverse the inequality sign.

Here is the graph of the solution:
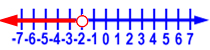
Let’s check our work. We need to substitute in a number for x that is less than -2. Let’s use -4.

2-Step Inequalities
Now, let’s put together everything we’ve learned.
Some inequalities require more than one step to solve. For example:
3x + 6 < 27
When you have both multiplication or division and addition or subtraction, undo the addition or subtraction first.
Let’s look at this example.

Here we check our work by substituting in a number for x that is less than 7. We’ll use 6.

Let’s do another one.
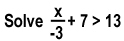
Remember that whenever we divide or multiply by a negative number, we need to flip the inequality sign.

Here we check our work by substituting in a number for x that is less than -18. We’ll use -21.

Here’s one more example.

Here we check our work by substituting in a number larger than 1 for x. We’ll use 2.