
Published by K12 Handhelds, Inc.
www.k12handhelds.com
Phone: 800-679-2226
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Monroe 2-Orleans BOCES.
Word Problems
When we use math in real life to solve problems, the problems aren’t given to us in an equation.
For example:
Suppose you want to buy three loaves of bread that cost $1.50 each and a jar of peanut butter that costs $4. A jar of jelly is $2.75, but you don’t need any jelly. You have $10. How much money will you have left over?
In order to solve this problem, you need to translate the words into numbers, so you can do the math to get the answer.
Here are the steps to solve a word problem:
- Read the problem and find out what is being asked.
- Identify any information that isn’t needed.
- Identify the information that is important to solving the problem.
- Write an equation by translating the words into numbers and symbols.
- Solve the equation.
- Check your work.
Let’s try this for the above problem.
First, what is being asked? The problem asks how much money will be left over after you buy bread and peanut butter.
What information isn’t needed. The cost of jelly is given, but since you don’t need any, that doesn’t matter. We can ignore that information.
What information is important to solving the problem? We need to know how much money we have ($10). We also need to know how much the things we’re buying cost (3 loaves of bread cost $1.50 each, and 1 jar of peanut butter costs $4).
Now we need to write an equation. This is a very important step. In order to write the equation, we need to translate the words into math symbols. Here are some hints that will help.
Use a variable, like x or n, to stand for information you don’t know (what you’re trying to find).
The following words indicate addition (+):
- plus
- sum
- more than
- greater than
- in addition
- and
- increase
- gain
- older
- bigger
- combined
The following words indicate subtraction (–):
- minus
- difference
- less than
- fewer than
- decrease
- loss
- have left
- younger
- smaller
The following words indicate multiplication (X or •):
- product
- times
- double (2•)
- triple (3•)
- of
- price/size/length of many things (if you know it for one)
The following words indicate division (÷):
- divided by
- a portion of
- half (÷ 2)
- quotient
- average
- split
- each
- price/size/length of one thing (if you know it for many)
The following words indicate equals (=):
- is
- equals
- is the same as
- you get
Let’s practice these now. For each of the words or phrases given, choose the math expression.
1. plus
2. double
3. is
4. less than
5. five fewer than
6. three pounds heavier than
7. split four ways
Let’s go back to our problem now:
You want to buy three loaves of bread that cost $1.50 each and a jar of peanut butter that costs $4. A jar of jelly is $2.75, but you don’t need any jelly. You have $10. How much money will you have left over?
Let’s make n the amount of money we have left over. “Left over” tells us that we need to do subtraction. In this case, we will subtract the amount spent from the amount we have. The amount spent is the sum (“and”) of the cost of the bread and the peanut butter. The cost of the bread can be found by multiplying (to find the price of many).
The cost of the bread is 3 • $1.50. The cost of the peanut butter is $4. We add those together to get the amount spent. Here is the final equation.
n = $10 – ((3 • $1.50) + $4)
Here is how we figured out the different parts:

We can then solve the problem to find that n = $1.50. This means that we will have $1.50 left.
Check your work by plugging in the numbers to solve the equation. You can also check to make sure that the answer makes sense by rereading the problem and seeing if $1.50 makes sense as an answer.
Let’s do another problem.
The star running back on our football team got most of his total yardage running. The rest was catching passes. He caught passes for 60 yards. His total yardage was 150 yards. The running back for the other team got 200 yards. How many yards did the star running back on our football team get running?
See if you can go through the steps to solve this problem and then write the equation yourself before going to the next page to see the answer.
OK. Let’s start with what we need to figure out. We are asked how many yards the running back got running. Let’s make that n.
The number of yards the other team’s running back got doesn’t matter, so we can ignore that information.
We know that the total for our running back was 150. Since that’s the total, we know that’s the answer to the equation. The running yards and the passing yards added together equals 150. And we know he caught passes for 60 yards.
So the equation is:
60 + n = 150
To solve for n:
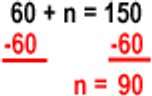
Our answer is that the running back ran for 90 yards. We can check this by reading the problem and substituting the numbers. He caught passes for 60 yards and ran for 90 yards. This gives a total of 150 yards, which matches the original problem.
Here’s another word problem.
The average temperature in Lincoln in July is 85 degrees. Last Wednesday it was 90 degrees. Today it was 15 degrees cooler than last Wednesday. What was the temperature today?
See if you can go through the steps to solve this problem and then write the equation yourself before going to the next page to see the answer.
We can begin by ignoring the sentence about the average temperature. It doesn’t have anything to do with what we’re being asked, which is what the temperature today was.
We know that last Wednesday it was 90 degrees. We are told it is 15 degrees cooler today. Cooler means lower, so we need to subtract. If n is the temperature today, then:
n = 90 – 15
n = 75
The temperature today is 75 degrees.
For some problems, it may help to draw a picture. Let’s try this problem.
Julie’s yard is rectangular. One side of the yard is 100 feet wide. The total area of the yard is 3,000 square feet. What is the length of the other side of the yard?
We can draw a picture to begin.
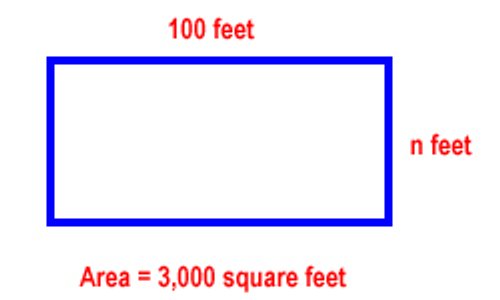
We know that the formula for area is:
Area = Length • Width
Now let’s substitute in the other information we know.
3,000 = 100 • n

The answer is that the length of the other side of the yard is 30 feet.
Try these on your own.
8. Joanna has 3 more books in her backpack than Sophie. If Sophie has n books, how many does Joanna have?
9. Martin has a business washing cars. Last year he washed 20 cars a week. This year, he wants to increase his business to 1,200 cars a year. How many cars will he have wash each month on average?
10. Michelle has $80 to buy a new outfit. She found a skirt for $20, a blouse for $25, and a belt for $8. How much does she have left to buy shoes?
11. In track last week, the boys ran sixteen laps. The girls ran four more laps. Each lap is a quarter of a mile. How many miles did the girls run?