Published by K12 Handhelds, Inc.
Long Beach, CA
www.k12handhelds.com
Phone: 800-679-2226

Copyright © 2005 by K12 Handhelds, Inc. License CC-by, Creative Commons License
This work is licensed under a Creative Commons Attribution 3.0 United States License.

Developed in conjunction with Wicomico County Schools.

Table of Contents

Introduction

Geometry is a kind of math that studies the relationships between lines, shapes, and three-dimensional figures. Geometry is important to many jobs. Builders use geometry to figure out how much lumber and other material they need. Scientists use geometry to calculate formulas. People use geometry to figure out how much fencing to buy or how much paint they need to paint a room.

Polygons

A polygon is a closed figure or shape with straight sides. Examples of polygons are squares and triangles. A circle is not a polygon because it has no straight sides.

Here are several types of polygons:

Triangle

A triangle has three sides.

Quadrilateral

A quadrilateral has four sides.

These are all quadrilaterals.

Square

A square is a quadrilateral that has four right angles and four sides that are all the same length.

Rectangle

A rectangle is a quadrilateral that has four right angles and opposite sides that are parallel.

Rectangle

Parallelogram

A parallelogram is a quadrilateral with opposite sides that are parallel and the same length.

Parallelogram

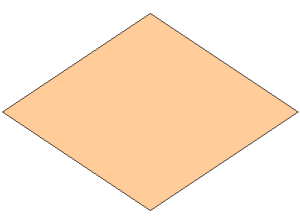
Rhombus

A rhombus is a quadrilateral with four sides that are the same length.

Rhombus

Trapezoid

A trapezoid is a quadrilateral with only two sides that are parallel.

Trapezoid

Pentagon

A pentagon is a polygon with five sides.

Pentagon

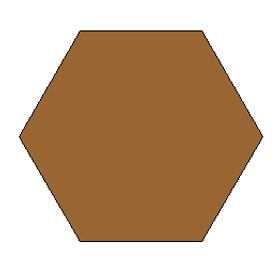
Hexagon

A hexagon is a polygon with six sides.

Hexagon

Octagon

An octagon is a polygon with eight sides.

Octagon

Perimeter is the distance around the outside of a shape. Adding the length of each side of a polygon will give you the perimeter. People often need to know the perimeter of something. For example, if you are going to buy fencing to go around your yard, you will need to know the perimeter.

Perimeter

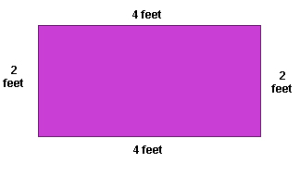
The perimeter of this rectangle is 12 feet. You can see this by adding the length of all the sides.

Perimeter = 4 feet + 2 feet + 4 feet + 2 feet

BONUS: The formula for calculating the perimeter of a rectangle is:

Perimeter = (2 x base)) + (2 x height)

The area of a shape is the amount of space inside of shape. Because area measures the space inside, it is measured in square units of measure, such as square inches or square miles. If you need to know how much carpet to buy for a room, you will need to calculate the area.

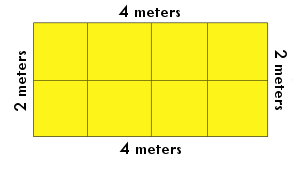
The area of this rectangle is 8 square meters. You can see this by counting the squares that fill the space.

BONUS: The formula for calculating the area of a quadrilateral is:

Area = base x height

Transformations

A transformation is a change in a shape, or a way of mapping the shape onto another space. Examples of transformations are slides, flips, and turns.

A slide, or translation, is moving a shape along a line. The shape is scooted over, like you’d slide a plate from one person to another. Here is an example of a slide:

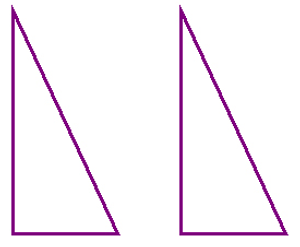
This picture shows a slide of a triangle.

A flip, or reflection, is a way of moving a shape across a line, producing a mirror image. It is like flipping a pancake. Here is an example of a flip:

This picture shows a flip of a triangle.

A turn, or rotation, is the turning or spinning a shape. It is like a person doing a cartwheel. Here is an example of a turn:

This picture shows a turn of a triangle.

Shapes that are congruent have the same shape and size. They could be slid, flipped, or turned and would then be exactly the same. These are examples of congruent shapes:

These shapes are congruent. They can be moved to be exactly the same.

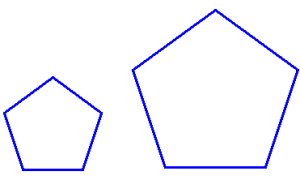
Shapes that are similar have the same shape, but may be different sizes. These are examples of similar shapes:

These shapes are similar. They are the same shape, but different sizes.

Some shapes can be tessellated. A tessellation of a shape is when the shape is repeated so that it covers a surface completely without leaving any space. Here is an example of a tessellation:

Tessellation

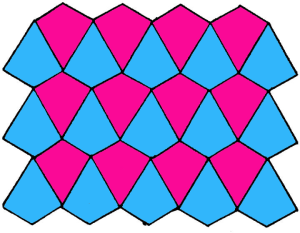
You can use the Tessellation program on your handheld to create your own tessellations.

Three-Dimensional Figures

Three-dimensional figures are figures in space that have length, width, and depth. They are solid objects like a cube, a sphere, or a pyramid. Sometimes three-dimensional is abbreviated as 3D. 3D movies are called that because objects on the screen seem to jump out like three-dimensional figures.

The sides of a three-dimensional figure are its flat surfaces. The edges are where the faces meet. The vertices are the corners or points where three or more surfaces meet.

Here are several types of three-dimensional figures:

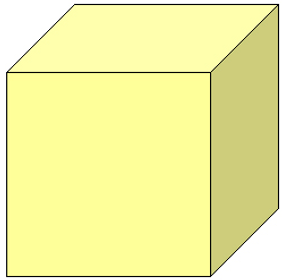
Cube

A cube is a three-dimensional figure with six identical square faces. All the sides of a cube are equal. All the faces are squares. Examples of a cube include dice and a block.

Cube

Sphere

A sphere is a round three-dimensional figure. Examples of a sphere include a ball and the earth.

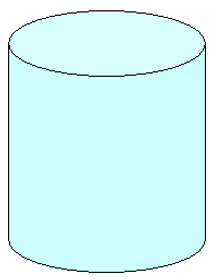
Cylinder

A cylinder is a three-dimensional figure with two flat circular faces. Examples of cylinders include a log and a drum.

Cylinder

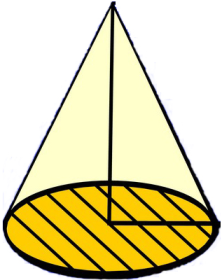
Cone

A cone is a three-dimensional figure with a circular flat base and another curved surface that goes up to a point. An example of a cone is an ice cream cone.

Cone

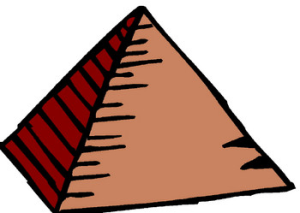
Pyramid

A pyramid is a three-dimensional figure with a flat polygon base and triangular surfaces that go up to a point. The ancient Egyptians built the famous stone pyramids in Egypt.

Pyramid

Prism

A prism is a three-dimensional figure with two faces that are parallel polygons and other faces that are parallelograms. A rectangular prism has two parallel rectangles. A triangular prism has two parallel triangles. An example of a rectangular prism is a box of cereal. The kind of glass prism you might use in science to bend light is a triangular prism.

This is a triangular prism.

The volume of a three-dimensional figure is the amount of cubic space inside the shape. Because volume measures the space inside, it is measured in cubic units of measure, such as cubic inches or gallons. If you need to know how much water will be needed to fill a swimming pool, you will need to calculate the volume.

BONUS: The formula for calculating the volume of a rectangular prism is:

Volume = length X width X depth

Glossary

area – the amount of space within a closed shape; the number of square units needed to cover a figure

base – the flat face on which a 3 dimensional figure can rest.

closed figure – a figure that starts and ends at the same point and has no open gaps

cone – a three-dimensional figure with a circular flat base and another curved surface that goes up to a point

congruent – having the same shape and same size

cube – a three-dimensional figure with six identical square faces

cylinder – a three-dimensional figure with two flat circular faces

edge – a line segment where two faces of a 3-dimensional figure meet.

face – a flat side of a three-dimensional figure

geometry – a field of math that studies the relationships between lines, shapes, and three-dimensional figures

hexagon – a polygon with six sides

line of symmetry – a line on which a figure can be folded so that both sides are the same

The red line shown here is the line of symmetry of this triangle.

net – a flat pattern that can be folded to make a three-dimensional figure

This is the net of a cube. If you cut out this pattern and folded it right, it would make a three

octagon – a polygon with eight sides

open figure – a figure that does not start and end at the same point.

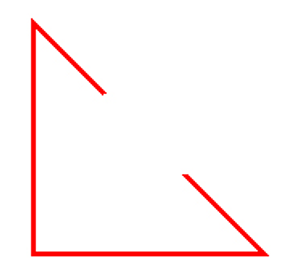
This is an open figure. It has a gap in it.

parallel – lines that are exactly the same distance apart and would never meet

parallelogram – a quadrilateral with opposite sides that are parallel and the same length

pentagon – a polygon with five sides

perimeter – the distance around the outside of an object or shape

polygon – a closed figure with straight sides

pyramid – a three-dimensional figure with a flat polygon base and triangular surfaces that go up to a point

The stone pyramids in Egypt were built by ancient Egyptians.

quadrilateral – a polygon with four sides

rectangle – a quadrilateral that has four right angles and opposite sides that are parallel

rectangular prism – a three-dimensional figure with two faces that are parallel rectangles and other faces that /g are also rectangles

reflection – flip; a movement of a figure across a line, producing a mirror image

rhombus – a quadrilateral with four sides that are the same length

right angle – an angle that is 90 degrees

This is a right angle. It is exactly 90 degrees and makes a square corner.

rotation – turn; the turning of a figure

side – a line that is a part of a polygon

similar – having the same shape, but possibly a different size

sphere – round three-dimensional figure; a ball

square – a quadrilateral that has four right angles and four sides that are all the same length

tessellation – repeated shapes that cover a flat surface without overlapping or leaving any gaps

three-dimensional figure – a figure in space that has length, width, and depth; it is a solid object

transformation – a change in a shape, or a way to mapping the shape onto another space; examples: translation, reflection, rotation

translation – slide; to move a figure along a line

trapezoid – a quadrilateral with only two sides that are parallel

triangle – a polygon with three sides

two-dimensional figure – a closed figure that has length and width; a flat object

vertex – the common point of three or more edges of a three-dimensional figure; plural form is vertices

The vertices of this cube are circled in red.

volume – the amount of 3dimensional space occupied by an object

Return to top